Note: this article is a short summary of a larger work I have done here.
Short introduction
Hyperspectral images are like ordinary images, except that they have lots of bands extended beyond the visible spectrum. This extra information is exploited for material identification. For example, in this hyperspectral image a sub-scene is selected – called the Alunite Hill.

The original Cuprite scene from which a 16 x 28 pixel subimage is extracted for analysis.
Subsequently, the ICE algorithm is run which results in the following three material abundance maps contained in matrix and material signatures
called endmembers.

Output of the ICE algorithm: abundance maps for alunite, muscovite and kaolinite minerals, and their hyperspectral signatures, i.e. endmembers.
ICE algorithm
Simplified, the ICE algorithm can be written as an objective function which measures the error between the actual pixels and the predicted pixels
together with a regularization term
that measures the size of the simplex formed by the endmembers.
This objective function is subsequently minimized to get the estimates of the abundance maps and endmembers:
Spatial information
The idea that spatial information is important stems from the fact that materials in abundance maps are more likely to reflect certain order.
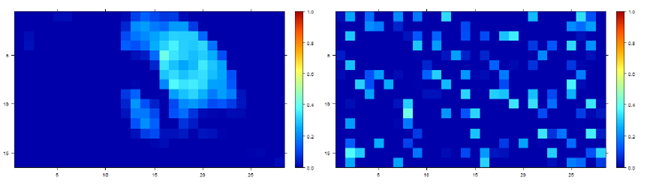
Two abundance maps of the same material. The pixels are identical, but randomly ordered in the right one.
Thus the right abundance map in which the material seems randomly scattered, should be penalized more than the left one where there seems to be a certain order. One way to achieve this is by looking at the adjacent pixels of the abundance maps and see how similar they are. In this specific approach we are calculating the variance of a pixel and its adjacent four pixels. These variances are summed over all pixels of the abundance maps:
where signifies the vector of the abundance and the adjacent abundances of the
-th pixel and
-th endmember. The new simplified objective functions becomes
This new objective function is then minimized:
The abundance maps resulting from the minimization of tend to be more smooth.

Output of ICE-S algorithm. The abundance maps are slightly more smooth when compared with the ICE output above. The central pixel in the third abundance map seems to be completely removed.
Conclusion
My main aspiration here was to give a very concise and simplified version of how the ICE algorithm can be extended with spatial information. The actual topic is much more complex. For those interested: The theoretical foundations, calculus and implementation details can be found here.