Analytical procedure validation based on product specification done right (USP 1033)

Note: this article is a short summary of a larger preprint paper.

The starting point of the USP 1033 guideline is the requirement to measure product potency within its specification limits during routine testing. Meanwhile, the pharmaceutical industry traditionally defines acceptance criteria for the measuring analytical procedure in terms of either accuracy and precision or total analytical error (TAE) and risk.

Every analyst and even USP 1033 authors struggle with reconciling these two concepts because it is not clear how to translate product requirements to procedure requirements. Latest (30-SEP-2024) USP 1033 draft addresses this by making a simplifying assumption: that the production process exhibits no variability, allowing product specifications to be directly expressed through TAE. In practice analysts then rely on these results (i.e. formulas) and add rule-of-thumb margins (e.g. Six Sigma) to account for actual process variability. However such approaches, often lacking a theoretical foundation, can break down in edge cases or lead to overly strict acceptance criteria.

All this raises an important question: can procedure acceptance criteria be correctly derived from product specifications? The answer is yes, but not in the traditional sense as global scalar limits. Based on some recent work and in line with USP 1033, I’ll explain here briefly the exact (!) method of assessing procedure performance based on product specifications. An example application is also available here.

The first step is spelling out the assumptions and abstracting them to a formal framework. From USP 1033 concepts and formulas we can deduce the following measurement model (and vice versa):

$M_{ij} := \mu_P\tau_XPB_iW_{ij} \sim \mathcal{LN}(\ln\mu_P + \ln\tau_X, \sigma_P^2 + \sigma_B^2 + \sigma_W^2 )$

where $\mu_P$ is the geometric center of the production process, $\tau_X$ the trueness factor (or multiplicative systematic error) of the procedure, and $P$ , $B_i$ and $W_{ij}$ the unit-centered lognormal random variables of respectively the production process variability ( $\sigma^2_P$ ), and the between and within run variability of the procedure ( $\sigma_B^2 + \sigma_W^2 = \sigma^2_{IP}$ ). Note that production process parameters (i.e. $\mu_P$ and $\sigma^2_P$ ) are assumed known and often set to some safe estimate (cf. USP 1033). Also note that procedure parameters $\tau_X$ , $\sigma_B^2$ and $\sigma_W^2$ are determined during validation at different levels of the true value and thus are a function of it. True value during routine measurement is the random variable $\mu_PP$ .

The second step is stating the problem to be solved which translates to:

$P(LSL < M < USL) \ge 1 - \omega$

or in layman’s terms: The probability to measure outside of product upper (USL) and lower (LSL) specification limit should not exceed $\omega$ . To make it more concrete, we can translate this into a comprehensible analytical target profile (ATP) which I base here on the latest (30-SEP-2024) USP 1033 draft example:

The procedure must be able to quantify relative potency (RP) in a range from 0.5 to 2 RP such that, under the assumed lognormal manufacturing distribution with $\mu$ = 1 RP and $\sigma$ = 0.048 RP, the expected probability of measured values (i.e. 1 run, 1 replicate) falling outside [0.70; 1.43] RP product specification limits is less than 1%.

The third step is then deriving from the second equation the acceptance limits for the procedure. This is where it becomes clear that there is no unique scalar solution for accuracy and precision, or TAE and risk due to the interactions between $\tau_{X}$ and $\sigma^2_{IP}$ and their dependence on the true value. (The suggested solutions in USP 1033 are ones-of-many and because of that may result in falsely rejecting a perfectly fine procedure.) More complex criteria are required. In the graph that follows the validation of the procedure is represented as a good compromise between complexity and intelligibility.

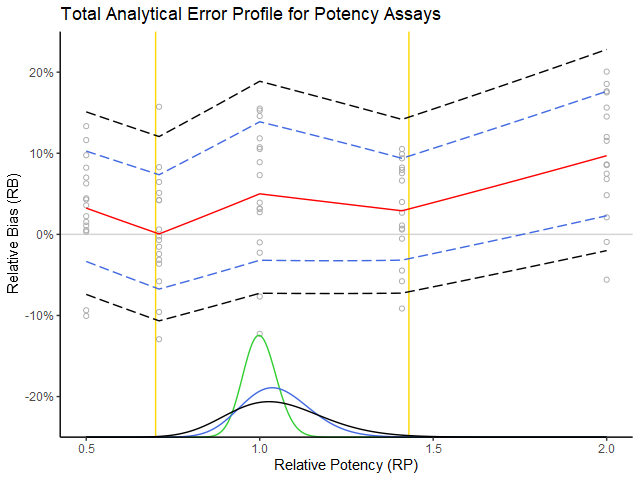
Overview of assay performance in function of the ATP.

Figure 1: The experimental measurements (grey circles) are plotted as relative error (%) in function of true relative potency (RP). The red curve is the expected relative bias (RB) and the blue dotted interval is the added intermediate precision (IP). (These estimates are taken from the USP 1033 tables.) One can state roughly that the blue dotted interval covers about 68 % of the measurements. The density curves below reflect the performance in routine. The green density represents the RP of the production process. The blue density tells us what will happen when we measure these products with our procedure (i.e. based on the procedure’s performance summarized with the blue dotted lines). One can see that the measurements would remain well within the boundaries of the product specification (i.e. the yellow bars). The black density has exactly 99 % of its area within the yellow bars, which then translates to the black dotted acceptance interval of the procedure as the maximal addition of global IP to the current performance (blue dotted lines) while still meeting the ATP requirements. Hence the difference between black and blue dotted lines can be interpreted as the maximal global IP that the procedure can incur while still remaining within the ATP specification.

The above graph represents an exact solution based on the assumptions in step 1 and step 2, which among others implies:
– that the procedure performance’s dependence on measurand’s true value is taken into consideration (hence the importance of interpolation of procedure performance estimates over the whole working range),
– that the (assumed) knowledge of the production process stated in the ATP is acknowledged by “weighting” the procedure’s performance importance based on the production process density,
– that lognormality (although hardly visible) is taken into account, etc.

The graph also can be made interactive (cf. here) so the analyst can adjust various components such as the product specifications, the production process, and procedure performance characteristics (locally or globally) and gain immediate feedback on its effect in routine use. This allows the analyst to find the best way (in terms of effort versus impact) to make the procedure fit for its purpose.

PS And yes, this methodology can be used within a larger framework of Integrated Process Modeling (IMP) and all this can also be applied to assays in general governed by ICH Q2(R2) by using a measurement model that is based on the normal distribution.

Leave a Reply Cancel reply